A projectile is an object upon which the only force acting is gravity. There are a variety of examples of projectiles: an object dropped from rest is a projectile (provided that the influence of air resistance is negligible), an object thrown vertically upwards is a projectile (provided that the influence of air resistance is negligible), and an object thrown upwards at an angle is also a projectile (the same assumption). A projectile is any object which, once projected, continues its motion by its own inertia and is influenced only by the downward force of gravity.
By definition, a projectile has only one force acting upon - the force of gravity. If there were any other force acting upon an object, then that object would not be a projectile. Projectiles can be launched both horizontally and vertically, and they have both horizontal and vertical velocity and horizontal and vertical displacement.
Formulas:
vertical velocity
vertical velocity at time initial vertical velocity acceleration of gravity time
vertical displacement
vertical displacement at time initial vertical velocity time - quadratic square root added time - quadratic square root subtracted acceleration of gravity
horizontal velocity
horizontal velocity at time
horizontal displacement
horizontal velocity at time initial horizontal velocity time
Range given projection angle and
equal initial and final elevations
range initial velocity acceleration of gravity A projectile is shot at an initial velocity v0 at an angle q above the horizon. How far will it go? How high will it rise? What is the shape of its trajectory?Denote the projectile's range R and the height of its trajectory h. Let us choose the origin of the coordinate system at the launch point, the x axis in the horizontal direction and the y axis in the vertical direction pointing up. Then the components of v0, the initial velocity vector, are The entire motion is described by the kinematics vector equations that prescribe the variation with time of position vector r and velocity vector v for a given acceleration vector a:
v0x = v0 cos q v0y = v0 sin q (1) Each vector equation is actually a set of two independent equations (this is a two dimensional motion) for the x and y components of the corresponding vectors. That is, these equations are simply shorthand notation for
dr/dt = v dv/dt = a So in reality we are dealing with two sets of independent equations for the x and y directions and can envision the problem as a superposition of two completely independent motions that together are equivalent to the projectile motion.
dx/dt = vx dvx/dt = ax dy/dt = vy dvy/dt = ay Let us consider two other objects. The first one moves in the horizontal direction with the constant velocity v0x. All the factors that govern the motion of this object and of the horizontal component of our projectile motion are identical. These two motions cannot be distinguished from each other. Therefore, if we solve for the motion of this imaginary object we will have solved the x component of the projectile motion. The second object we consider is thrown straight up with velocity v0y. All the factors that govern the motion of this object and of the vertical component of our projectile motion are identical. Again, if we solve for the motion of this imaginary object we will have solved the y component of the projectile motion. These two imaginary objects will become our projectile when we link their motions with a common time because in the projectile case, both the horizontal and vertical motions start at the same place at the same time. Our projectile is equivalent to an object moving up and down, and also sliding in the horizontal direction while executing this vertical motion.
We can easily find the total duration of the vertical component of the motion; you may wish to revisit the relevant note on up-and-down motion to refresh your memory and see how that's done. Once we know how long the projectile stayed in the air, finding the range from the horizontal motion is simple. Let's put these ideas together.
The Horizontal Component
Neglecting air resistance, the velocity x component does not change throughout the entire motion. Therefore, vx = v0x andThat's all for the horizontal motion.
x = v0x t (2) The Vertical Component
The y component of the projectile's motion is subject to the gravitational acceleration which points downward. So vy as a function of time isfor our choice of axes. You may wish to revisit the note on the choice of signs for velocity and acceleration. The y motion can be envisioned as an object thrown straight up with velocity v0y. Such an object will rise until its velocity is zero, so from the last equation the time to reach maximum height is
vy = v0y - g t (3) The object will then fall to the ground and the downward trip is the mirror image of the trip up; you may wish to revisit the relevant note. Therefore, the total time the object stays in the air is
tmax = v0y/g (4) Putting it Together
ttot = 2tmax = 2v0y/g (5)
That's it. We have derived the total duration of the projectile's motion. To find the range R, all that is left is to plug ttot into equation (2) which gives us the distance covered at any time t. The result iswhere in the last step we inserted v0x and v0y from equation (1).
R = v0xttot = 2v0xv0y/g = 2(v02/g) sin q cos q (6) Why the funny dependence on angle? From the first step in equation (6), the range is the product of the horizontal velocity component and the total duration of the motion. For a given launch speed v0, large v0x are obtained at small launch angeles. But then the duration of the flight is short because v0y is small. Conversely, a steep launch angle will maximize the duration of the motion by giving a large v0y, but then v0x is small and the object simply goes up and down without getting very far. The competition between these two opposing effects is the reason for the q dependence shown in our result. This result can be simplified when we recall the identity from trigonometry sin2q = 2sinq cosq. With this identity, the range becomes simply
The maximum value of the sine function is 1, obtained when its argument is p/2 (90°). Therefore, for a given v0, the maximal range is v02/g, obtained for a launch angle q = 45°. The function sinq is symmetric about its peak at 90°, therefore the function sin2q is symmetric about 45°. For example, a projectile launched at 30° will have the same range as one launched at 60°.
R = (v02/g) sin2q (7) The Trajectory Height
An object thrown upward with velocity v0y will rise to a height v0y2/2g; you may wish to revisit the note on up-and-down motion to verify this result. So this is the height of the projectile's trajectoryThe Trajectory Shape
h = v0y2/2g = (v02/2g) sin2q
At any time t, the y coordinate obeysfor our choice of y axis (check again the note on the choice of signs). From equation (2) we can eliminate time in terms of horizontal distance, t = x/v0x. With this replacement, equation (7) is transformed into a relation for y as a function of x
y = v0yt - ½ g t2 (7) where the coefficients A and B are
y = Ax - Bx2 Verify these results for yourself, performing the replacement t = x/v0x in equation (7). The function we just derived shows that y has a quadratic dependence on x, namely, the trajectory is a parabola. y vanishes at x = 0 and x = A/B. Can you figure out the meaning of these two zeroes of the function?
A = tanq B = ½ g/(v0 cosq)2
EXAMPLES of PROJECTILE MOTION PROBLEMS:
1. A golf ball is projected with a horizontal velocity of 30 m/s and takes 4.0 seconds to reach the ground. (Assume g= 10 m/s² and the air resistance is negligible.) Calculate: the height from which the golf ball was projected. The magnitude of the golf balls' vertical velocity component just before hitting the ground. The horizontal velocity component. Resultant velocity just before the object strikes the ground. The horizontal component of the object's displacement.
2. Erica kicks a soccer ball 12 m/s at an angle of 40 degrees above the horizontal.
a. What is the ball's maximum height?
b. What is the ball's maximum range?
c. With what velocity does the ball strike the ground?
d. What are the ball's acceleration and velocity at the top of its rise?
ANSWERS :
1. assigning "+" to down we have:
horizontal vertical distance ? ? acceleration 0 10 m/s2 initial velocity 30 m/s 0 m/s final velocity ? ? time 4.0 s 4.0 s
a. To find the horizontal displacement at 4.0 s :
d = vivt + (0.5)at2 where viv = 30, t = 4.0 and a = 0 . Solve for d
b. To find the horizontal component of velocity at 4.0 s :
vfh = vih + at = 30 m/s + 0 = 30 m/s
c. To find the vertical component of the velocity at 4.0 s :
vfv = viv + at = 0 + (10)(4.0) = 40 m/s
d. The resultant velocity at 4.0 s is
√(302 + 402) = 50 m/s
ø = tan-1(40/30) = 53º below the horizontal
e. The vertical displacement at 4.0 s is:
d = vivt + (0.5)at2 where viv = 0, t = 4.0 and a = 10 . Solve for d
2. First, find the components of the initial velocity:
viv = 12sin40º = 7.71 m/s (+ is assigned up)
vih = 12cos40º = 9.19 m/s
so far, we have:
horizontal vertical distance ? ? acceleration 0 -9.8 m/s2 initial velocity 9.19 m/s 7.71 m/s final velocity ? ? time ? ?
a. We can find the time it takes the ball to rise to the top of its trajectory by assigning zero to the final vertical velocity.
a = ( vfv - viv)/t or, t = ( vfv - viv)/a
t = ( 0 - 7.71)/(-9.8) = 0.7867 s
The maximum height is given by
d = vivt + (0.5)at2
d = 7.71(0.7867) + (0.5)(-9.8)(0.7867)2 = 3.03 m
b. To find the time for the whole trip double the time it takes the ball to go only up. Also the time of travel is the same in both the vertical and horizontal components.
t = 2 x 0.787 s = 1.57 s
Now we have:
horizontal vertical distance ? ? acceleration 0 -9.8 m/s2 initial velocity 9.19 m/s 7.71 m/s final velocity ? ? time 1.573 s 1.573 s
The range is the horizontal distance traveled:
d = viht + (0.5)at2
d = 9.19(1.57) + (0.5)(0)(1.57)2 = 14.4 m
c. To find the velocity of the ball as it strikes the ground, we find the final velocity in each component and add them as vectors.
In the horizontal component:
a = ( vfh - vih)/t or
vfh = vih + at = 9.19 m/s + 0 = 9.19 m/s
In the vertical component,
a = ( vfv - viv)/t or,vfv = viv + at = 7.71 + (-9.8)(1.573) = -7.71 m/s or 7.71 m/s [down]
Adding the two components together the velocity with which the ball strikes the ground is:
9.19 m/s [horizontal] + 7.71 m/s [down] = 12.0 m/s 40 º below the horizon.
d. At the top of its rise the ball's velocity is 9.19 m/s horizontally and its acceleration is 9.8 m/s2
vibien
jeric
chesa
diana
anna
john michael
meyer
pj
charles

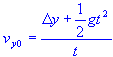
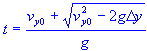
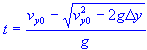


0 comments:
Post a Comment